Flavor Equilibration Module
This module provides code to calculate physics quantities related to beta equilibration, which includes beta equilibration rates, warm beta equilibrium charge fraction, relaxation rates, susceptibilities, bulk viscosity and damping time.
How to Use
How to Run the Code
Option 1: Using Docker Interactively
Docker provides a platform-independent way of running the module. Docker needs to be installed first.
To clone the flavor_equil repository, go to the directory you want and run
git clone https://gitlab.com/nsf-muses/flavor-equilibration/beta_equil
cd beta_equil
Then build the Docker image,
docker build -t feq:dev .
Run the Docker image,
docker run --rm -it feq:dev
Option 2: Without Using Docker
Clone the flavor_equil repository
git clone https://gitlab.com/nsf-muses/flavor-equilibration/beta_equil
cd beta_equil
Required Python packages: - numpy - scipy - matplotlib - pandas - vegas : Monte-Carlo integration module https://pypi.org/project/vegas/
Option 3: Using Calculation Engine
[Under development]
Docker needs to be installed first, and make sure Docker is running.
To run the workflow of this individual module, first clone the git repo and change directory
git clone git@gitlab.com:nsf-muses/flavor-equilibration/beta_equil.git /tmp/beta_equil
cd /tmp/beta_equil
run the bash script by
sh test/run_module.sh
How to Change/Add Inputs
The input EoS files should be generated by the software pipeline and placed into the input folder. Or you can manually paste an EoS file in the folder.
Parameters of the calculation (e.g. number of Monte Carlo points for the integral, range of density and temperature to be covered, etc) are specified in the input/config.yaml file.
Structure of the Code
Flow of the Flavor_Equil Module
As shown in the flowchart below, the module takes as input a tabulated equation of state (EoS) for neutral matter. This table must be indexed by \(n_B,T,Y_Q\).
There are then two possible calculations (“missions”) the code can perform. The mission is specified in the config.yaml file.
“getFlavorEquilInfo”. The EoS_Neutral_Matter module calculates necessary susceptibilities and add them to the table. The code then loops through the requested values of \(n_B,T\) (specified in config.yaml) and for each it calculates certain linear-response properties of equilibrated matter, such as equilibrium charge fraction, equilibrium isospin chemical potential, relaxation rate, static bulk viscosity.
“getUrca”. The code loops through the requested values of \(n_B,T,Y_Q\) (specified in config.yaml) and for each one it calculates direct and modified Urca rates and the net rate.
Flowchart
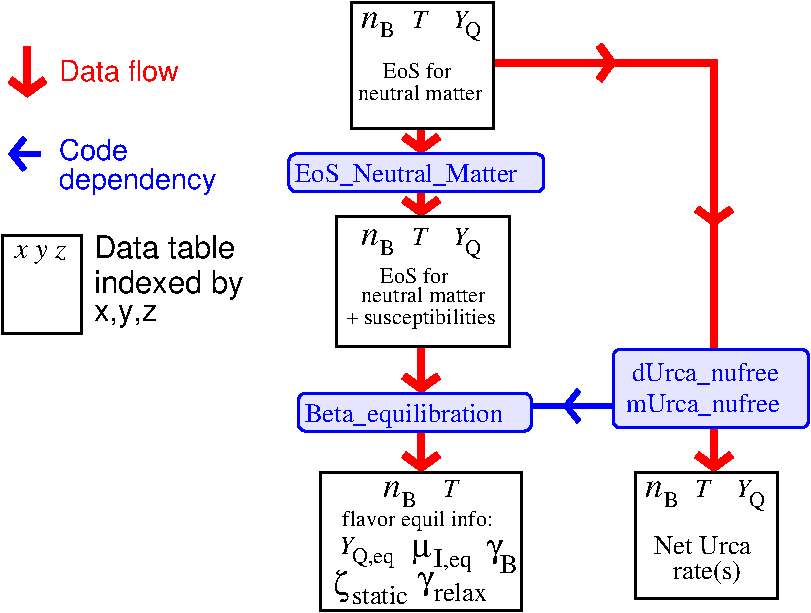
Flowchart of general algorithm and data transformations
Documentation for Each Python Module
Explain in full detail all of the input and output options.
The structure and the component of the module is listed as the following:
Porter_adaptors.py Functions that convert an EoS table from Porter format to this module’s native format, and converts the output to Porter format
EoS_Table_nTY.py Base class for any class that is read in an EoS table indexed by (\(nB,T,YQ\)). It provides functions that linearly interpolate the tabular data
EoS_Neutral_Matter_nTY.py (inherits from EoS_Hadrons_nTY) A class to store an EoS for electrically neutral n+p+e matter, and calculate properties including susceptibiities relevant to bulk viscosity. Properties are provided to the user as functions of \(nB\), \(T\), and \(YQ\)
dUrca_nufree.py (inherits from EoS_Hadrons_nTY) A class that calculates the rate of direct Urca beta equilibration processes.
dUrca_nufree_FSA.py (inherits from EoS_Hadrons_nTY) A class that calculates the rate of direct Urca under Fermi surface approximation.
mUrca_nufree_FSA.py (inherits from EoS_Hadrons_nTY) A class that calculates the rate of modified Urca processes.
Beta_Equilibration.py (inherits from EoS_Neutral_Matter_nTY) A class that calculates beta equilibration properties such as the equilibriu charge fraction, relaxation rate, bulk viscosity.
Dockerfile A dockerfile to containerize this module and build the image of this module. The image should be platform-independent
Constants.py A set of useful physical constants and conversion factors
Utilities.py A set of useful functions for testing agreement, numerical derivatives, simple plotting, robust root-finding, etc.
calculate_Urca_rates.py A script that calculates Urca rates.
calculate_flavor_equilibration_properties.py A script that calculates the flavor equilibration properties (bulk viscosity etc).
Scientific Motiviation
Neutron star mergers probe high density, low to intermediate temperature part of the QCD phase diagram. People use mergers to study properties of dense matter, and an important aspect of studying the merger is the equilibration dynamics. This module provides code to calculate properties related to flavor equilibration in the neutrino-transparent regime, where the temperature is below 10 MeV.
We consider a fluid element consisting of neutrons, protons and electrons. While the fluid element is experiencing density oscillations, the weak interaction trys to bring the matter back to beta equilibrium in which the charge fraction remains unchanged.
The reactions involved are neutron decay and electron capture:
where \(N\) stands for spectator nucleons. The set of reactions is called direct Urca without spectator nucleons, and modified Urca with spectator nucleons.
The equilibrium condition for the neutrino-transparent regime is described by
where \(\mu_I^{eq}\) the isospin chemical potential. It is calculated by setting the net rate (net of total neutron decay and total electron capture) equal 0. [1]
With the presence of a small-amplitude density oscillation, the density oscillation and the weak interaction are competing, which leads to a resonance pheonmenon known as bulk viscosity,
The static bulk visocsity is \(\zeta_0 = - \frac{\partial p}{\partial x_I}\biggr|_{n_B} \frac{\gamma_B}{\gamma_I^2}\) and p is the pressure. \(\gamma_I\) is the isospin relaxation rate that tells how quickly the matter is acting in response to a change in \(x_I\), and similar for \(\gamma_B\).
When the isospin relaxation rate is large compared to oscillation frequency \(\omega\), the matter is fast equilibrated. When it is smaller than \(\omega\), the matter barely equilibrates. In between, our study suggests [2] that the relaxation timescale \(\tau = 1/\gamma_I\) is comparable to that of the merger. Therefore, including the Urca processes into the dynamics is necessary.
For detailed discussions on the isospin chemical potential, see [1].
For detailed discussions on the isospin equilibrium, see [2].
References
[1] M. G. Alford, A. Haber, S. P. Harris and Z. Zhang, Beta Equilibrium Under Neutron Star Merger Conditions, Universe 7 (2021) 399, arXiv:2108.03324.
[2] M. G. Alford, A. Haber, and Z. Zhang, Isospin Equilibration in Neutron Star Mergers, Phys. Rev. C109, 055803 (2024), arXiv:2306.06180.