Physics overview

The present code provides two dimensional QCD equations of state (EoS) in the \((T,\mu_B)\) plane at \(\mu_Q = \mu_S = 0\), with a critical point marking the separation between a crossover at low \(\mu_B\) and \(1^{st}\) order phase transition at high \(\mu_B\) [1]. The location of the critical point is not predicted, but left free to choose by the user along a given parametrized transition line, as well as the parameters shaping the critical region.

To construct the complete EoS, lattice QCD data coupled to HRG data (for the low temperature part) are used to compute an EoS using the \(T'\)-expansion scheme, which is then merged to a critical part mapped to QCD coordinates from a 3D Ising model at the level of the scaling temperature \(T'\).

Lattice \(T'\)-Expansion Scheme

The \(T'\)-Expansion Scheme (TExS) provides a relationship between \(\chi_1^B\) and \(\chi_2^B\) through the following main identity:

\[\frac{T}{\mu_B}\chi_1^B(T,\mu_B) = \chi_2(T',0) \; ,\]

where the scaling temperature \(T'(T,\mu_B)\) is given as an expansion in powers of \(\mu_B/T\) by the formula:

\[T'(T,\mu_B) = T\left[1 + \kappa_2^B(T)\left(\frac{\mu_B}{T}\right)^2 + ... \right] \; .\]

It enables thus to compute the baryon density \(n_B \equiv \chi_1^B\) at finite baryon chemical potential from the \(2^{nd}\) order baryon susceptibility at \(\mu_B=0\), using the scaling temperature \(T'(T,\mu_B)\) [2]. In the construction used here, \(\chi_2^B\) is obtained from parametrizing a combination of HRG data [3] for \(T \leq 120\) MeV, and lattice QCD data from [4] above. The expansion parameter \(\kappa_2\) of the \(T'\) expansion is also parametrized from HRG at low-\(T\), and from lattice data from [1] above \(T = 120\) MeV.

Mapping Ising to QCD

In order include the contribution of a critical point, a non-universal mapping from \((r,h) \longleftrightarrow (T, \mu_B)\) is achieved, in two steps. To ensure that the transition of the Ising model \((h=0)\) is aligned with the QCD crossover line, this transformation can be simplified by mapping Ising coordinates \((r,h)\) to alternative scheme coordinates \((T',\mu_B)\) as:

\[\frac{T' - T_0}{T_C T'_{,T}} = -w' h \sin\alpha'_{12} \; ,\]
\[\frac{\mu_B^2 - \mu_{BC}^2}{2\mu_{BC}T_C} = w' (-r\rho' - h \cos\alpha'_{12}) \; .\]

From there, one can recover the regular \((T, \mu_B)\) coordinates of QCD through the definition of the scaling temperature \(T'\).

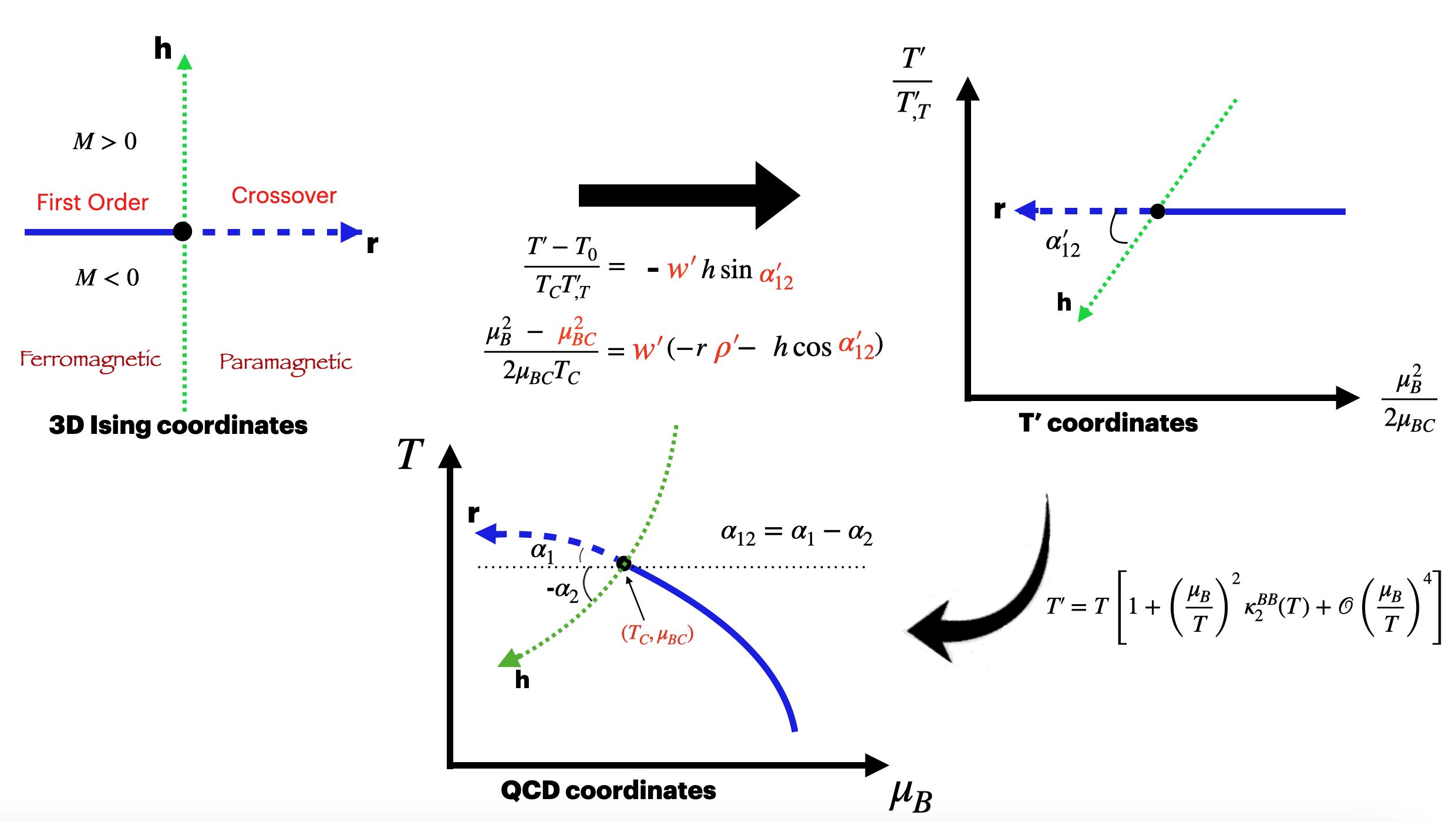
"Mapping from 3D Ising model to QCD"

Schematic description of the mapping of a critical point from 3D Ising model coordinates to actual QCD coordinates \(T\) and \(\mu_B\), through an intermediary step using the scaling temperature \(T'\) and rescaled squared baryon chemical potential.

Merging Ising with lattice TExS

To ensure that the temperature scaling reproduces lattice results at low \((\mu_B/T)\), and that the critical component from the Ising model only contributes at higher orders in \((\mu_B/T)\), we use:

\[T'(T,\mu_B) = \underbrace{T'_{\text{lat}}(T,\mu_B)}_{\text{lowest orders in }(\mu_B/T)} + \underbrace{T_{\text{crit}}(T,\mu_B) - \text{Taylor}[T_{\text{crit}}(T,\mu_B)]}_{\text{higher order in }(\mu_B/T)} \; ,\]

where

\[T'_{\text{crit}}(T,\mu_B) \approx T_0 + \left(\frac{\partial \chi^B_{2,\text{lat}}(T,0)}{\partial T}\Big|_{T_0}\right)^{-1} \frac{n^{\text{crit}}_B(T,\mu_B)}{T^3(\mu_B/T)}f(T,\mu_B)\]

Using the TExS main identity, we can then compute baryon density \(n_B(T, \mu_B) \equiv \chi_1^B(T, \mu_B)\) for the full EoS. From there, we calculate all thermodynamic observables, starting from \(2^{nd}\) order baryon susceptibility:

\[\frac{\chi_2(T,\mu_B)}{T^2} = T\left(\frac{\partial(n_B/T^3)}{\partial \mu_B}\right)\bigg|_{T}\]

and pressure:

\[\frac{P(T,\mu_B)}{T^4} = \chi_{0,\text{lat}}^B(T,0) + \frac{1}{T}\int_0^{\mu_B} \frac{n_B(T,\mu_{B}^\prime)}{T^3} d\mu_{B}^\prime \; ,\]

from which we obtain entropy density:

\[\frac{s(T,\mu_B)}{T^3} = \frac{1}{T^3}\frac{\partial P(T,\mu_B)}{\partial T}\Big|_{\mu_B}\]

and finally energy density:

\[\frac{\epsilon(T,\mu_B)}{T^4} = - \frac{P(T,\hat{\mu}_B)}{T^4} + \frac{s(T,\hat{\mu}_B)}{T^3} + \hat{\mu}_B\frac{n_B(T,\hat{\mu}_B)}{T^3}\]

References