QLIMR Module

Welcome to the documentation for the QLIMR module, a computational tool designed to obtain gravitational observables of rotating neutron stars. The acronym ‘QLIMR’ stands for Quadrupole moment (Q), Love number (L), Moment of inertia (I), Mass (M), and Radius (R) of the star. This module offers a comprehensive framework for studying the properties of neutron stars from the gravitational perspective, based on a barotropic Equation of State (EoS) provided by the user. In the following sections, you will find all the relevant information, including installation instructions, practical usage guidelines, and detailed explanations of the computations, providing you with a comprehensive guide to harnessing the capabilities of the QLIMR module.

Introduction

Neutron stars are extremely compact objects studied within the context of general relativity. However, obtaining exact analytical solutions for isolated rotating neutron stars has proven elusive. Numerical relativity simulations, while powerful, come with significant computational expenses. This prompts the utilization of the perturbative approach of Hartle and Thorne, which offers a more manageable way to gain valuable insights on the physics and dynamics of these intriguing objects.

This module uses such approach as the cornerstone to numerically solve the perturbation equations from which one can extract different gravitational properties of neutron stars. The code is intended to be a great tool for the scientific community interested in studying and computing gravitational observables using a massive number of EoSs. When provided with a specific EoS and a defined set of input parameters, QLIMR is capable of generating two types of output variables. The first category encompasses the local functions derived from solving the equations, while the second category comprises the global variables, such as the star’s mass and radius, which serve as key observables.

The following sections serve as essential guides for users. The ‘Installation’ section outlines the process of setting up the module in their computational environment. ‘Mathematical Foundations’ delves into the theoretical groundwork, elucidating the theoretical aspects underpinning the modelling of rotating neutron stars. ‘Code Architecture and Structure’ provides insight into the organization of the QLIMR code, offering a clear overview of its components. The ‘Usage Workflow’ section guides users through the entire process, from input specification to output results, streamlining its integration into research workflows. Lastly, ‘Examples’ offers practical demonstrations, showcasing QLIMR’s functionalities and empowering users with hands-on experience in studying neutron stars.

Installation

This section outlines the essential steps to prepare your environment for running the code seamlessly. We’ll begin by detailing the system requirements, ensuring your system meets the necessary specifications. Next, we’ll guide you through the installation of libraries and dependencies that are required for execution. Following that, you’ll find comprehensive instructions for setting up your environment, offering options for Docker container installation, local host installation, and also campus cluster setup. Choose the method that aligns best with your preferences and get ready to dive into QLIMR.

Docker container installation

The easiest way to run QLIMR is through a Docker container. Docker provides a consistent environment for running applications, ensuring QLIMR’s dependencies are met regardless of the host system. Before proceeding, ensure Docker is installed on your local machine. You can find detailed installation instructions here.

Setup

Clone the QLIMR repository from the command line:

git clone https://gitlab.com/nsf-muses/ns-qlimr/qlimr.git

Navigate to the cloned repository directory:

cd qlimr

Building the Docker Container

Execute the following command to build the QLIMR Docker container:

bash build_container.sh

If the MUSES common container needs to be updated, use the following command:

docker pull registry.gitlab.com/nsf-muses/common/muses-common:latest

The instructions to build the image are provided in the Dockerfile. Please note that typically, building the Docker container is a one-time task unless you need to make modifications to the source code.

Local host installation

Another option for running QLIMR is on your local machine rather than using a container. To do this, certain libraries and dependencies are necessary. Ensure that your local machine has a modern version of the g++ GNU compiler installed, along with Python and the following dependencies:

numpy, pandas, PyYAML, openapi-core and muses_porter .

  • yaml-cpp is a human-readable data serialization standard that can be used in conjunction with all programming languages and is often used to write configuration files. QLIMR uses .yaml format files for reading the inputs and generating the outputs. They are used to facilitate the data transfer between different modules.

  • GNU Scientific Library is a versatile mathematical toolkit developed by the GNU Project for C and C++ and provides a wide set of mathematical functions and algorithms. QLIMR integrates the GSL library due to its exceptional performance ensuring efficient and accurate solutions for tasks involving interpolation, numerical integration, and solving ordinary differential equations.

Setting up your environment

For users intending to execute QLIMR on a local machine, it is required to install the mentioned libraries. The installation procedure may vary depending on the operating system (OS) being employed.

Linux

YAML Installation

# Ubuntu / Debian:
sudo apt-get update
sudo apt-get install libyaml-cpp-dev

# CentOS / Fedora:
sudo dnf install yaml-cpp-devel

# Arch Linux:
sudo pacman -S yaml-cpp

# openSUSE:
sudo zypper install yaml-cpp-devel

# Alpine Linux:
sudo apk add yaml-cpp-dev

# YAML for python across all Linux distributions
pip install --upgrade pip
pip install pyyaml

GSL Installation

# Ubuntu / Debian:
sudo apt-get update
sudo apt-get install libgsl-dev

# CentOS / Fedora:
sudo dnf install gsl-devel

# Arch Linux:
sudo pacman -S gsl

# openSUSE:
sudo zypper install gsl-devel

# Alpine Linux:
sudo apk add gsl-dev

macOS

For macOS users, utilizing the package manager Homebrew offers an efficient approach for installing the required libraries. In case Homebrew is not yet installed, it can be obtained using the following commands in a new terminal.

# Homebrew Installation
/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"

# Check Homebrew version
brew --version

YAML Installation

# YAML Library for C++
brew install yaml-cpp

# YAML Library for python
pip install pyyaml
GSL Installation 

brew install gsl

These dependencies are essential for running QLIMR locally. Make sure they are installed on your system before proceeding.

Building QLIMR locally

Navigate to the src folder first by typing on a terminal

cd src

Then, to build qlimr, run:

make redo

If you’re using a macOS with an M1 chip, you can run:

bash build_qlimr_M1.sh

This build_qlimr_M1.sh script is designed to handle compilation for the M1 chip, which may require different compiler settings or optimizations. Additionally, it’s worth noting that the user typically only needs to build QLIMR once, unless they intend to modify the source code to achieve specific results.

Mathematical Foundations

Hartle-Thorne procedure

The Hartle-Thorne procedure is a technique used to derive an approximate solution for neutron stars that are rotating at a slow rate. The underlying concept involves introducing small disturbances to an exact solution representing a non-rotating, spherically symmetric star. This serves as the base configuration known as the background spacetime. The dimensionless expansion parameter ($\epsilon$) in this context is the ratio between the angular speed ($\Omega$) of the star, and the angular speed at which mass shedding would occur ($\Omega_{\textrm{K}}$). The model relies on the following assumptions:

  1. Equation of State: In the non-rotating configuration, matter follows a barotropic equation of state represented as $p=p(\varepsilon)$, where $p$ denotes the pressure and $\varepsilon$ stands for the total energy density. In conditions of extremely high densities as in the interior of NS, the Fermi temperature ($T_{\textrm{f}} \sim 3 \times 10^{11} \textrm{K} $) greatly surpasses the temperature of the star, resulting in an EoS which is unaffected by the star’s temperature. Thus, the main contribution to the pressure is due to nuclear forces and corrections caused by thermal agitation can be neglected.

  1. Matter distribution: The matter distribution of the star in the non-rotating configuration is described by a perfect-fluid stress energy tensor. Shear stresses and energy transport are negligible.

  1. Axial and reflection symmetry: The perturbed spacetime that characterizes the rotating star exhibits axial symmetry with respect to an arbitrary axis, which is assumed to be aligned with the star’s rotation axis. Moreover, the geometry remains unchanged when mirrored across a plane perpendicular to the axis of rotation. These symmetry properties allow for setting the structure of the geometry and enable the decoupling of Einstein’s Equations, as elaborated upon below.

  1. Uniform rotation: Although differential rotation can be considered, uniformly rotating configurations are assumed, as they represent stable states that minimize the total mass-energy.

  1. Slow rotation: The non-rotating metric configuration is perturbed in a dimensionless small spin parameter $\epsilon = \Omega / \Omega_{\textrm{K}}$. In this context, $\Omega$ represents the angular speed of the neutron star as observed from spatial infinity, while $\Omega_{\mathrm{K}}$ is a characteristic frequency defined by $\Omega^{2}{\mathrm{K}} = M{\star}/R_{\star}^{3}$, where $R_{\star}$ and $M_{\star}$ refer to the radius and the mass-energy in the non-rotating configuration. The quantity $\Omega_{\mathrm{K}}$ corresponds to the Keplerian orbital frequency of a test particle at a radius $R_{\star}$ moving around a mass $M_{\star}$. Thus, $\Omega_{\mathrm{K}}$ is interpreted as the mass shedding frequency. Therefore, the approximation is valid for $\epsilon \ll 1$, but breaks down when $\epsilon \sim 1$.

As mentioned earlier, the Hartle-Thorne procedure relies on the perturbation of an exact background metric. Therefore, we define a one-parameter family of metrics $g_{\alpha \beta}(\epsilon)$ as

$$ \begin{equation} g_{\alpha \beta} = g^{\textsf{B}}{\alpha \beta} , + , \epsilon h^{(1)}{\alpha \beta} , + , \frac{1}{2!} \epsilon^{2} h^{(2)}_{\alpha \beta} , + , \cdots \end{equation} $$

The quantity $g^{\textsf{B}}_{\alpha \beta}$ is the static and spherically symmetric background metric defined as

$$ \begin{equation} ds_{\textsf{B}}^{2} \equiv g^{\textsf{B}}_{\alpha \beta} dx^{\alpha}dx^{\beta} = -e^{\nu(r)} dt^{2} + e^{\lambda(r)} dr^{2} + r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2}) \end{equation} $$

According to the symmetry assumptions, the perturbed metric can be expanded up to $\mathcal{O}(\epsilon^{2})$ as []

$$ \begin{align} ds^{2} =& -e^{\nu(r)} \big[ 1 + 2 \epsilon^{2}h_{2}(r,\theta) \big] dt^{2} + e^{\lambda(r)} \left[ 1 + \dfrac{2 \epsilon^{2} m_{2}(r,\theta)}{r - 2 M(r)} \right] dr^{2} \[1ex] &+ r^{2} \big[ 1 + 2 \epsilon^{2}k_{2}(r,\theta) \big] \bigg( d\theta^{2} + \sin^{2}\theta \big[ d\phi - \epsilon \omega_{1}(r,\theta) dt \big]^{2} \bigg) \end{align} $$

where $\omega_{1}$ denotes a first order correction while $h_{2}$, $m_{2}$ and $k_{2}$ correspond to second order corrections in the spin parameter ($\epsilon$). The form of the metric is justified by symmetry arguments. Note that for an axially symmetric spacetime a transformation of the form $\Omega \rightarrow - \Omega$ is equivalent to $t \rightarrow -t$. Therefore, $g_{t\phi}$ should contain only odd powers of $\epsilon$ and $g_{tt}$, $g_{rr}$, $g_{\theta\theta}$, $g_{\phi\phi}$ only even powers. From this metric ansatz, the perturbations $h^{(1)}{\alpha \beta}$ and $h^{(2)}{\alpha \beta}$ are therefore,

$$ \begin{align} h^{(1)}{\alpha \beta} dx^{\alpha}dx^{\beta} &= 2 r^{2} \omega{1}(r,\theta) \sin^{2}\theta dt d\phi , , , \[1ex] h^{(2)}{\alpha \beta} dx^{\alpha}dx^{\beta} &= - \bigg[ 4 e^{\nu(r)} h{2}(r,\theta) + 2 r^{2} \sin^{2}\theta \omega_{1}(r, \theta)^{2} \bigg] dt^{2} + 4 e^{\lambda(r,\theta)} \frac{m_{2}(r,\theta)}{r-2 M(r)}dr^{2} \[1ex] &+ 4 r^{2} k_{2}(r,\theta) \left( d\theta^{2} +\sin^{2}\theta d\phi^{2} \right) , . \end{align} $$

The slow rotation perturbations will also produce corrections to the stress-energy tensor which is considered to be a perfect fluid given by

$$ \begin{equation} T_{\alpha \beta} = (\varepsilon + p )u_{\alpha}u_{\beta} + pg_{\alpha \beta} \end{equation} $$

The pressure $p$, the total energy density $\varepsilon$ and the four-velocity $u^{\alpha}$ would change in the interior of the rotating star. Therefore, we define a one-parameter family of perturbed quantites as,

$$ \begin{align} p(\epsilon) &= p^{\textsf{B}}(r) + \epsilon p^{(1)}(r,\theta) + \frac{1}{2!} \epsilon^{2}p^{(2)}(r,\theta) \[1ex] \varepsilon(\epsilon) &= \varepsilon^{\textsf{B}}(r) + \epsilon \varepsilon^{(1)}(r,\theta) + \frac{1}{2!} \epsilon^{2}\varepsilon^{(2)}(r,\theta) \[1ex] u_{\alpha}(\epsilon) &= u_{\alpha}^{\textsf{B}}(r) + \epsilon u_{\alpha}^{(1)}(r,\theta) + \frac{1}{2!} \epsilon^{2}u_{\alpha}^{(2)}(r,\theta) \end{align} $$

$$ \begin{equation} T_{\alpha \beta} = T^{\textsf{B}}{\alpha \beta} , + , \epsilon T^{(1)}{\alpha \beta} , + , \frac{1}{2!} \epsilon^{2} T^{(2)}_{\alpha \beta} , + , \cdots \end{equation} $$

Zeroth Order in $\Omega$

$$ \begin{equation} ds^{2} = -e^{\nu(r)} dt^{2} + e^{\lambda(r)} dr^{2} + r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2}) \end{equation} $$

$$ \begin{equation} e^{\lambda(r)} = \left[ 1 - \dfrac{2M(r)}{r} \right]^{-1} \ . \end{equation} $$

r-formulation

$$ \begin{align} \dfrac{dM}{dR} &= 4 \pi R^{2} \varepsilon \[3ex] \dfrac{d\nu}{dR} &= 2 \dfrac{M + 4\pi R^{3} p}{R(R-2 M)} \[3ex] \dfrac{dp}{dR} &= -(\varepsilon + p)\dfrac{M + 4\pi R^{3} p}{R(R-2 M)} \end{align} $$

$$ \begin{align} \dfrac{dM}{dR} &= 4 \pi R^{2} \varepsilon \[3ex] \dfrac{d\nu}{dR} &= 2 \dfrac{M + 4\pi R^{3} p}{R(R-2 M)} \[3ex] \dfrac{dp}{dR} &= -(\varepsilon + p)\dfrac{M + 4\pi R^{3} p}{R(R-2 M)} \end{align} $$

h-formulation

Let $h=\ln\textsf{h}$ and then $dh=\dfrac{d \textsf{h}}{\textsf{h}} = \dfrac{dp}{\varepsilon + p}$

$$ \begin{align} \dfrac{dM}{dh} &= - \dfrac{4 \pi \varepsilon R^{3} (R-2M)}{M + 4 \pi R^{3} p} \[3ex] \dfrac{dR}{dh} &= - \dfrac{R(R-2M)}{M + 4\pi R^{3} p} \[3ex] \dfrac{d\nu}{dh} &= -2 \end{align} $$

where $p = p(h)$ and $\varepsilon = \varepsilon(h)$.

Initial conditions:

$$ \begin{align} R(h_{\epsilon}) &= R_{\epsilon} \[1ex] M(h_{\epsilon}) &= \dfrac{4 \pi}{3} \varepsilon_{c}R_{\epsilon}^{3} \end{align} $$

with $h_{\epsilon} = h_{c} - \dfrac{2 \pi}{3} R_{\epsilon}^{2}(\varepsilon_{c} + p_{c})$.

First Order in $\Omega:$

$$ \begin{equation} ds^{2} = -e^{\nu(r)} dt^{2} + e^{\lambda(r)} dr^{2} + r^{2}\bigg( d\theta^{2} + \sin^{2}\theta \big{ d\phi - \epsilon \big[ \Omega - \omega_{1}(r,\theta) \big] dt \big}^{2} \bigg) \end{equation} $$

$$ \begin{equation} \dfrac{d^{2}\omega_{1}}{dR^{2}} + 4 \dfrac{1-\pi R^{2}(\varepsilon + p)e^{\lambda}}{R} \dfrac{d\omega_{1}}{dR} - 16\pi (\varepsilon + p) e^{\lambda} \omega_{1} = 0 \end{equation} $$

Initial condition:

$$ \begin{equation} \omega_{1}(R_{\epsilon}) = \omega_{c} + \dfrac{8 \pi}{5} (\varepsilon_{c} + p_{c}) \omega_{c} R_{\epsilon}^{2} + \mathcal{O}(R_{\epsilon}^{2}) \end{equation} $$

Second Order in $\Omega:$

$$ \begin{align} ds^{2} =& -e^{\nu(r)} \big[ 1 + 2 \epsilon^{2}h_{2}(r,\theta) \big] dt^{2} + e^{\lambda(r)} \left[ 1 + \dfrac{2 \epsilon^{2} m_{2}(r,\theta)}{r - 2 m(r)} \right] dr^{2} \[1ex] &+ r^{2} \big[ 1 + 2 \epsilon^{2}k_{2}(r,\theta) \big] \bigg( d\theta^{2} + \sin^{2}\theta \big{ d\phi - \epsilon \big[ \Omega - \omega_{1}(r,\theta) \big] dt \big}^{2} \bigg) \end{align} $$

$$ \begin{align} m_{2} = & - Re^{-\lambda} h_{2} + \dfrac{1}{6}R^{4}e^{-(\nu + \lambda)} \left[ R e^{-\lambda} \left( \dfrac{d\omega_{1}}{dR} \right)^{2} + 16\pi R \omega_{1}^{2} \left( \varepsilon + p \right) \right] \[3ex] \dfrac{dK_{2}}{dR} = & - \dfrac{dh_{2}}{dR} + \dfrac{R-3M-4\pi p R^{3}}{R^{2}} e^{\lambda} h_{2} + \dfrac{R - M + 4\pi p R^{3}}{R^{3}}e^{2 \lambda} m_{2} \[3ex] \dfrac{dh_{2}}{dR} = & - \dfrac{R-M+ 4\pi p R^{3}}{R} e^{\lambda} \dfrac{dK_{2}}{dR} + \dfrac{3-4\pi(\varepsilon + p)R^{2}}{R} e^{\lambda} h_{2} + \dfrac{2}{R} e^{\lambda} K_{2} \[1ex] & + \dfrac{1+8\pi p R^{2}}{R^{2}} e^{2\lambda} m_{2} + \dfrac{R^{3}}{12}e^{-\nu} \left( \dfrac{d\omega_{1}}{dR} \right)^{2} \end{align} $$

Tidal Deformability and Love number

The ODE for the $\ell$-th multipole is given by

$$ \begin{align} &R \dfrac{dy}{dR} + y(y-1)+\dfrac{2}{f} \left[ 1 - \dfrac{3M}{R} - 2 \pi R^{2} (\varepsilon + 3p ) \right] y \[2ex] &- \dfrac{1}{f}\left[\ell(\ell+1)-4 \pi R^{2}(\varepsilon+p)\left(3 + \dfrac{d\varepsilon}{dp} \right)\right] = 0 \end{align} $$

Initial condition

$$ \begin{equation} y(R=0)=\ell \end{equation} $$

Love number $k_{2}$:

$$ \begin{align} \begin{split} k_{2} =& \dfrac{8}{5}(1-2C)^{2} C^{5}\left[ 2C(Y-1) - Y + 2 \right] \ &\times \bigg{ 2C \bigl[ 4(Y+1) C^{4} + (6Y-4) C^{3} + (26-22 Y)C^{2} \[1ex] & + 3(5Y-8) C- 3Y + 6 \bigr] - 3(1-2C)^{2} \bigl[ 2C(Y-1) \ &- Y + 2 \bigr] \ln \left( \dfrac{1}{1-2C} \right) \bigg}^{-1} \end{split} \end{align} $$

where $C= M/R$ is the compactness of the neutron star.

Numerical approach

Mathematical symbols and code variable mapping

Source Code Architecture and Structure

Design overview

How the code works

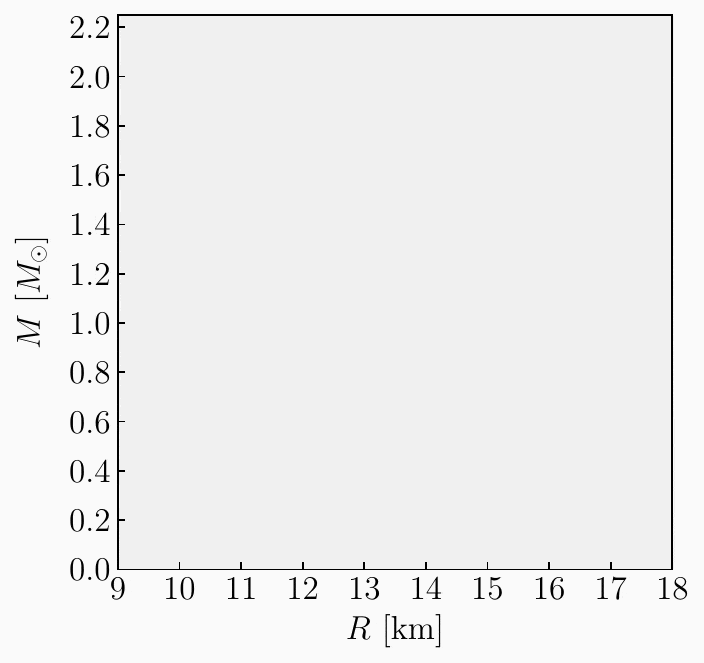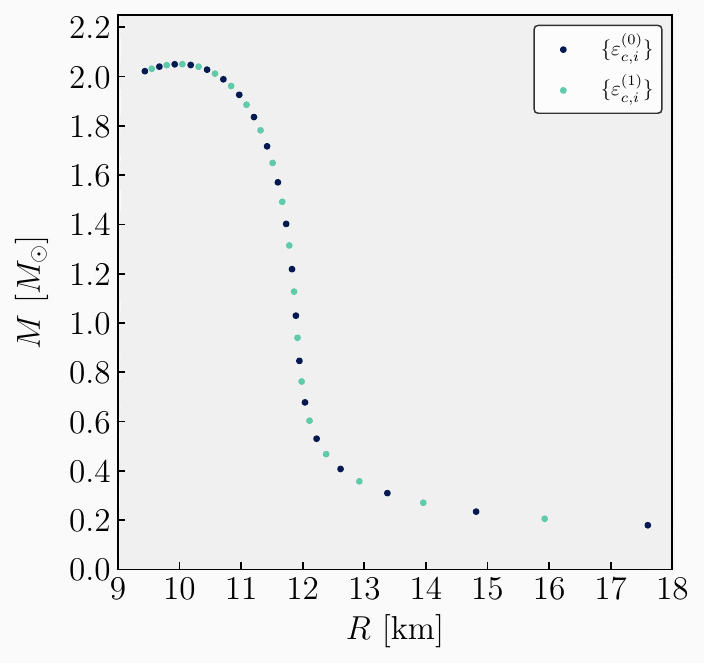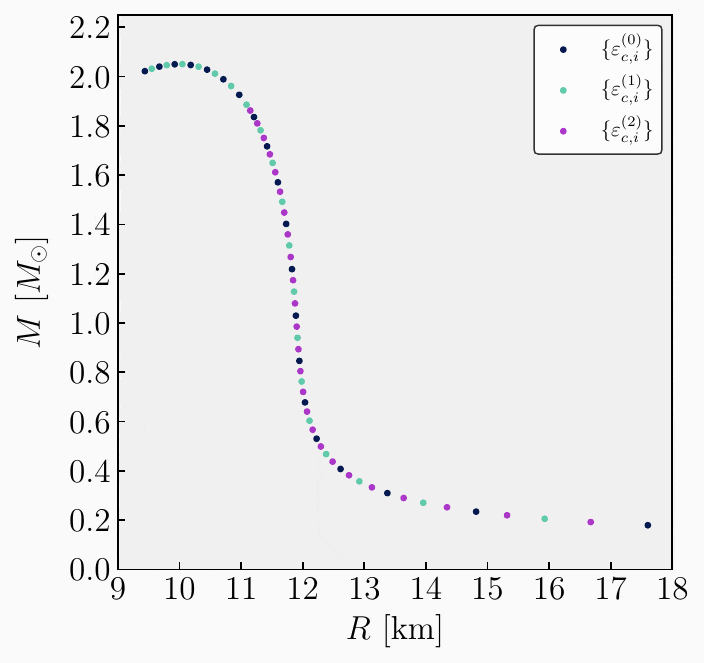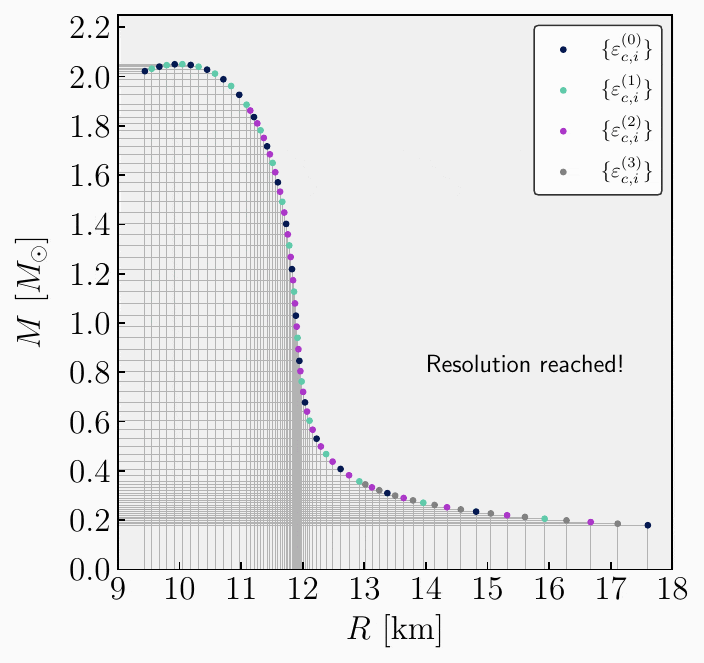
Alt Text

Header-Implementation Organization

Code diagram

Alt Text

Module’s Workflow

Alt Text

Input specifications

Running the code

Output results

Troubleshooting

Examples and Use Cases

CMF Example

Appendices

Exterior solutions

$$ \begin{align} \varepsilon^{\mathsf{ext}}(R) = p^{\mathsf{ext}}(R) = 0 \end{align} $$

$$ \begin{align} M^{\mathsf{ext}}(R) = M_{\star} \end{align} $$

$$ \begin{align} \nu^{\mathsf{ext}}(R) = -\lambda^{\mathsf{ext}}(R) = \ln \left( 1 - \frac{2 M_{\star}}{R} \right) \end{align} $$

$$ \begin{align} \varpi^{\mathsf{ext}}_{11}(R) = \Omega - \frac{2 S}{R^{3}} = \Omega \left( 1 - \frac{2 I}{R^{3}} \right) \end{align} $$

$$ \begin{align} h^{\mathsf{ext}}{22}(R) = \frac{1}{M{\star} R^{3}}\left( 1+\frac{M_{\star}}{R} \right)S^{2} + A Q^{2}{2}\left( \frac{R}{M{\star}} - 1 \right) \end{align} $$

$$ \begin{align} k^{\mathsf{ext}}{22}(R) = - \frac{1}{M{\star} R^{3}}\left( 1+\frac{2M_{\star}}{R} \right)S^{2} + \frac{2 A M_{\star}}{\sqrt{R(R-2M_{\star})}}Q^{1}{2}\left( \frac{R}{M{\star}} - 1 \right) - A Q^{2}{2} \left( \frac{R}{M{\star}} - 1 \right) \end{align} $$

$$ \begin{align} m^{\mathsf{ext}}{20}(R)=-\frac{S^{2}}{R^{3}} + \delta M{\star} \end{align}

$$

List of symbols

|

Symbol
|
Description
| |———-|———-| |
$t$ | Time coordinate in Boyer-Linquist type coordinates | |
$r$ | Radial coordinate in Boyer-Linquist type coordinates | |
$\theta$ | Polar angle in Boyer-Linquist type coordinates | |
$\phi$ | Azimuthal angle in Boyer-Linquist type coordinates | |
$\mathsf{h}$ | Enthalpy per rest mass-energy | |
$h$ | Pseudo-enthalpy defined as $h = \ln \mathsf{h}$. Independent integration variable | |
$h_{c}$ | Pseudo-enthalpy defined exactly at the center of the NS | |
$h_{\epsilon}$ | Pseudo-enthalpy at the small core of radius $\epsilon$ from the center of the NS | |
$R$ | Radial coordinate in Hartle-Thorne coordinates | |
$\Theta$ | Polar angle in Hartle-Thorne coordinates ($\Theta \equiv \theta$) | |
$R_{\epsilon}$ | Radial coordinate in Hartle-Thorne coordinates at small core of radius $\epsilon$ | |
$\epsilon$ | Book-keeping parameter of the Hartle-Thorne approximation | |
$g_{\mu \nu}$ | Axially symmetric full spacetime metric tensor| |
$g^{\mathsf{B}}{\mu \nu}$ | Spherically symmetric background metric tensor| |
$h{\mu \nu}$ | Metric perturbation tensor | |
$u^{\mu}$ | Fluid 4-velocity vector of the NS | |
$T_{\mu \nu}$ | Perfect fluid stress-energy tensor | |
$\nu$| Background metric function found in $g_{tt}$ | |
$\nu^{\textsf{ext}}$| Function $\nu$ valid only outside the NS | |
$\lambda$ | Background metric function found in $g_{rr}$| |
$\lambda^{\textsf{ext}}$ | Function $\lambda$ defined only outside the NS | |
$M$ | Enclosed mass-energy function related to $\lambda$ as $M \equiv (1-e^{-\lambda})r/2$ | |
$f$ | Schwarzschild function given by $f \equiv 1-2M/R$ | |
$p$ | Pressure function at the interior of the NS | |
$p_{c}$ | Pressure at exactly the center of the NS | |
$\varepsilon$| Total energy density function at the interior of the NS | |
$M_{\star}$| Total mass-energy of the NS | |
$R_{\star}$| Radius of the NS | |
$C$ | Compactness of the NS defined as $C \equiv M_{\star} / R_{\star}$ | |
$\Omega$ | Constant angular speed of the NS | |
$\omega_{1}$ | Metric function perturbation at $\mathcal{O}(\epsilon)$ found in $g_{t\phi}$| |
$\varpi_{1}$ | Relative angular velocity at order $\mathcal{O}(\epsilon)$ defined as $\varpi_{1} \equiv \Omega - \omega_{1}$ | |
$\varpi_{11}$ | Mode $\ell = 1$ function from the vector harmonic decomposition of $\varpi_{1}$ | |
$\varpi_{11,c}$ | Defined as $\varpi_{11}$ evaluated exactly at the center of the NS| |
$\varpi^{\mathsf{ext}}{11}$ | Function $\varpi{11}$ valid only at the exterior of the NS | |
$S$ | Angular momentum of the NS | |
$I$ | Moment of inertia of the NS| |
$\bar{I}$ | DImensionless moment of inertia defined as $\bar{I} \equiv I / M^{3}{\star}$ | |
$\xi{2}$| Radial displacement function away from sphericity | |
$\xi_{20}$| Mode $\ell = 0$ function from spherical harmonic decomposition of $\xi_{2}$ at $\mathcal{O}(\epsilon^{2})$| |
$\xi_{22}$ | Mode $\ell = 2$ function from spherical harmonic decomposition of $\xi_{2}$ at $\mathcal{O}(\epsilon^{2})$| |
$\xi_{20,c}$| Defined as $\xi_{20}$ evaluated exactly at the center of the NS | |
$h_{2}$ | Metric function perturbation found in $g_{tt}$ at $\mathcal{O}(\epsilon^{2})$ | |
$h_{20}$| Mode $\ell = 0$ function from spherical harmonic decomposition of $h_{2}$ at $\mathcal{O}(\epsilon^{2})$ | |
$h_{20,c}$| Defined as $h_{20}$ evaluated at exactly the center of the NS| |
$h_{22}$| Mode $\ell = 2$ function from spherical harmonic decomposition of $h_{2}$ at $\mathcal{O}(\epsilon^{2})$ | |
$h^{\mathsf{ext}}{22}$| Function $h{22}$ defined only at the exterior of the NS| |
$K_{2}$| Areal radius metric funciton perturbtion at $\mathcal{O}(\epsilon^{2})$| |
$K_{22}$| Mode $\ell = 2$ function from spherical harmonic decomposition of $K_{2}$ at $\mathcal{O}(\epsilon^{2})$ | |
$K^{\mathsf{ext}}{22}$ | Function $K{22}$ defined only at the exterior of the NS| |
$A$| Integrtion constant which appears in $h^{\mathsf{ext}}{22}$ and $K^{\mathsf{ext}}{22}$ | |
$B$| Initial condition constant in $h_{22}$ and $K_{22}$ system of differential equations | |
$m_{2}$| Metric function perturbation found in $g_{rr}$ at $\mathcal{O}(\epsilon^{2})$ | |
$m_{20}$| Mode $\ell = 0$ function from spherical harmonic decomposition of $m_{2}$ at $\mathcal{O}(\epsilon^{2})$ | |
$m^{\mathsf{ext}}{20}$| Function $m{20}$ defined only at the exterior of the NS| |
$m_{22}$| Mode $\ell = 2$ function from spherical harmonic decomposition of $m_{2}$ at $\mathcal{O}(\epsilon^{2})$ | |
$m^{\mathsf{ext}}{22}$| Function $m{22}$ defined only at the exterior of the NS | |
$y$| Tidal deformability function related to $h_{22}$ as $y \equiv R_{\star} h’{22}/h{22}$ | |
$Y$| Tidal deformability function related $y$ | |
$k_{2}$| Tidal apsidal constant | |
$\lambda^{\textsf{(tid)}}$| Tidal Love number of the NS | |
$\bar{\lambda}$| Dimensionless tidal Love number | |
$Q$| Rotational quadrupole moment | |
$\bar{Q}$| Dimensionless rotational quadrupole moment | |
$\delta R_{\star}$| Monopole correction to the radius of the NS | |
$\delta M_{\star}$| Monopole correction to the mass-energy of the NS |

Units

Geometrized units are often used in general relativity where $G=c=1$. For neutron stars, it is convenient also to set $M_{\odot}=1$. So, the overall units are $G=c=M_{\odot}=1$. This is the system of units used in QLIMR. That is equivalent to make all quantities dimensionless with respect to one solar mass in units of length ($\ell_{\odot} \simeq 1.5 $ $\mathsf{km}$). The following table shows the non-geometrized dimensions (NGD), geometrized dimensions (GD), neutron star dimensions (NSD) and the conversion factors between them for all the relevant quantities (Q) used in the source code.

|

Q
|
NGD
|
GD
|
NGD $\rightarrow$ GD
|
GD $\rightarrow$ NGD
|
NGD $\rightarrow$ NSD
|
NSD $\rightarrow$ NGD
| | :—:| :—:| :—:| :—:| :—:| :—:| :—:| |
$\varepsilon_{c}$ |
$\mathsf{L}^{-1}\mathsf{T}^{-2}\mathsf{M}$ |
$\mathsf{L}^{-2}$ |
$G/c^{4}$|
$c^{4}/G$ |
$G \ell^{2}{\odot}/c^{4}$ |
$c^{4}/G \ell^{2}{\odot}$ | |
$R_{\star}$ |
$\mathsf{L}$ |
$\mathsf{L}$ |
$1$ |
$1$ |
$1/\ell_{\odot}$ |
$\ell_{\odot}$| |
$M_{\star}$ |
$\mathsf{M}$ |
$\mathsf{L}$ |
$G/c^{2}$ |
$c^{2}/G$ |
$G/\ell_{\odot}c^{2}$ |
$\ell_{\odot}c^{2}/G$ | |
$I$ |
$\mathsf{L}^{2}\mathsf{M}$ |
$\mathsf{L}^{3}$ |
$G/c^{2}$ |
$c^{2}/G$ |
$G/\ell_{\odot}^{3}c^{2}$|
$\ell_{\odot}^{3}c^{2}/G$ | |
$\lambda^{\textsf{(tid)}}$ |
$\mathsf{L}^{2}\mathsf{T}^{2}\mathsf{M}$ |
$\mathsf{L}^{5}$ |
$G$|
$1/G$ |
$G/\ell^{5}{\odot}$ |
$\ell^{5}{\odot}/G$ |
$Q$ |
$\mathsf{L}^{2}\mathsf{M}$ |
$\mathsf{L}^{3}$ |
$G/c^{2}$|
$c^{2}/G$ |
$G/\ell^{3}{\odot}c^{2}$ |
$\ell^{3}{\odot} c^{2}/G$ | |
$\delta R_{\star}$ |
$\mathsf{L}$ |
$\mathsf{L}$ |
$1$ |
$1$ |
$1/ \ell_{\odot}$ |
$\ell_{\odot}$ | |
$\delta M_{\star}$ |
$\mathsf{M}$ |
$\mathsf{L}$ |
$G/c^{2}$|
$c^{2}/G$ |
$G/ \ell_{\odot}c^{2}$ |
$\ell_{\odot}c^{2}/G$ | |
$h$ |
- |
- |
- |
- |
-|
-| |
$R$ |
$\mathsf{L}$ |
$\mathsf{L}$ |
$1$ |
$1$ |
$1/ \ell_{\odot}$ |
$\ell_{\odot}$ | |
$\varepsilon$ |
$\mathsf{L}^{-1}\mathsf{T}^{-2}\mathsf{M}$ |
$\mathsf{L}^{-2}$ |
$G/c^{4}$ |
$c^{4}/G$ |
$G\ell_{\odot}^{2}/c^{4}$ |
$c^{4}/G\ell_{\odot}^{2}$ |
$p$ |
$\mathsf{L}^{-1}\mathsf{T}^{-2}\mathsf{M}$ |
$\mathsf{L}^{-2}$ |
$G/c^{4}$ |
$c^{4}/G$ |
$G\ell_{\odot}^{2}/c^{4}$ |
$c^{4}/G\ell_{\odot}^{2}$ |
$\nu$ |
- |
- |
- |
- |
-|
-| |
$Y$ |
- |
- |
- |
- |
-|
-| |
$\Omega$ |
$\mathsf{T}^{-1}$ |
$\mathsf{L}^{-1}$ |
$1/c$ |
$c$ |
$\ell_{\odot}/c$ |
$c/\ell_{\odot}$ |
|
$\varpi_{1}$ |
$\mathsf{T}^{-1}$ |
$\mathsf{L}^{-1}$ |
$1/c$ |
$c$ |
$\ell_{\odot}/c$ |
$c/\ell_{\odot}$ |
|
$\xi_{2}$ |
$\mathsf{L}$ |
$\mathsf{L}$ |
$1$ |
$1$ |
$1/ \ell_{\odot}$ |
$\ell_{\odot}$ | |
$h_{2}$ |
- |
- |
- |
- |
-|
-|
|
$K_{2}$ |
- |
- |
- |
- |
-|
-| |
$m_{2}$ |
$\mathsf{M}$ |
$\mathsf{L}$ |
$G/c^{2}$|
$c^{2}/G$ |
$G/ \ell_{\odot}c^{2}$ |
$\ell_{\odot}c^{2}/G$ |

References

[1] Hartle, J. B. (1967). Slowly rotating relativistic stars. I. Equations of structure. The Astrophysical Journal, 150, 1005.

[2] Lindblom, L. (1992). Determining the nuclear equation of state from neutron-star masses and radii. The Astrophysical Journal, 398, 569-573.

[3] Hartle, J. B., & Thorne, K. S. (1968). Slowly rotating relativistic stars. II. Models for neutron stars and supermassive stars. The Astrophysical Journal, 153, 807.

[4] Yagi, K., & Yunes, N. (2013). I-Love-Q relations in neutron stars and their applications to astrophysics, gravitational waves, and fundamental physics. Physical Review D, 88(2), 023009.

[5] Binnington, T., & Poisson, E. (2009). Relativistic theory of tidal Love numbers. Physical Review D, 80(8), 084018.

[6] Hinderer, T. (2008). Tidal Love numbers of neutron stars. The Astrophysical Journal, 677(2), 1216.