Architecture

This section provides a clear overview of the module’s structure, focusing on its main parts and how they work together. It includes three key subsections: Dependencies, which lists the necessary libraries and tools; Components, which describes the important pieces of the module; and Source Code, which explains how the moduele’s physics calculations are implemented.

The module’s source code is written in C++, supported by two Python layers—one for preparing the data and another for postprocessing. The entire application is wrapped in a Python script called qlimr.py, where users can input their parameters as flag arguments. This script can be executed on a local machine or within a Docker container.

In the Source Code subsection, detailed information about the implementation, including inputs and outputs is provided to describe how the module operates.

Dependencies

A description of each required library for the Python layers and the C++ source code is provided. If the module is run through Docker, these libraries are included in the Docker image. For users planning to execute the module on a local machine, please refer to the Execution section for detailed information on local installation.

Python Libraries

• NumPy is a powerful library for Python that simplifies working with numerical data. It provides support for large, multi-dimensional arrays and matrices, along with a collection of mathematical functions to perform operations on these arrays efficiently.

• pandas is a versatile library for Python that makes working with structured data easy. It provides powerful data structures, like DataFrames, which are similar to tables in a spreadsheet or SQL database.

• PyYAML is a Python library that makes it easy to work with YAML, a human-readable data serialization format. It allows you to easily parse YAML files into Python objects and convert Python objects back into YAML format.

• openapi-core is a Python library that simplifies working with OpenAPI specifications. It allows you to easily validate and interact with API requests and responses based on OpenAPI definitions.

• muses_porter Is a Python library developed for the MUSES Collaboration cyberinfrastructure to handle .csv and .hdf5 formats and column conventions.

C++ Libraries

• yaml-cpp is a human-readable data serialization standard that can be used in conjunction with all programming languages and is often used to write configuration files. The C++ source code uses .yaml format files for reading the inputs specified by the user and outputs a status.yaml file after execution.

• GNU Scientific Library is a versatile mathematical toolkit developed by the GNU Project for C and C++ and provides a wide set of mathematical functions and algorithms. QLIMR integrates the GSL library due to its exceptional performance ensuring efficient and accurate solutions for tasks involving interpolation, numerical integration, and solving ordinary differential equations.

Components

In this section, the basic structure of the code is explained, focusing on its use within a Docker container. This helps avoid compatibility issues across different operating systems and their dependencies. First, an overview of the Dockerfile will be provided, which sets up the container with the necessary tools and libraries, including a method to reduce the image size. Next, qlimr.py will be introduced as the script that the user interacts with, which contains an internal workflow consisting of five main steps: creating a user configuration file, validating input data, preprocessing the EoS data, executing the C++ code, and postprocessing the results.

Docker container

A Docker container is a lightweight, portable environment that allows applications to run consistently across different operating systems. By using a container, conflicts with dependencies that may arise from variations in system configurations are avoided.

Inside the module’s repository, there is a file called Dockerfile, which is a script containing instructions to set up the container with all the necessary dependencies for the module. The Dockerfile follows a multi-stage approach to minimize the size of the final image by including only what is essential. This method not only reduces the image size but also speeds up the building process. The multi-stage process includes three main parts:

Note

1. Building qlimr. In this stage, a common MUSES image is pulled, designed for use by all modules and containing basic packages like yaml-cpp and make. The GSL library is then installed, which is required for compiling the source code. Next, the /test and src/ folders are copied into the image. Finally, the QLIMR source code is compiled.

2. Installing Python dependencies. This Dockerfile stage starts by pulling a slim Python 3.11 base image. It references a requirements.txt file from the module’s repository, which outlines the necessary Python dependencies as detailed in the dependencies subsection above. To accommodate dependencies hosted on Git, Git is then installed. After updating the package list and installing Git, the package lists are removed to optimize space. Finally, the requirements.txt file is copied into the image, and the specified Python dependencies are installed.

3. Final image setup. In this final stage, a slim Python 3.11 base image is used to set up the final image. It installs make, defines a user with a specified UID, and creates a home directory at /opt. The stage then installs previously compiled Python and C++ dependencies from earlier stages, along with the source code, unit tests, API files, documentation, and other necessary files. It also creates input and output directories, and sets the working directory to /opt/src.

Once the Dockerfile is written following the three previously explained stages, it can be used to build the container. The final image for this module is approximately 300 MB. It’s important to note that the final output will be synchronized with the local host folder through Docker volumes, allowing for easy access to input and output data. For more information on how to build and run the container, please refer to the execution section.

Internal Workflow

The internal workflow of the module is executed when the user runs qlimr.py with specified arguments. In this context, qlimr.py acts as a wrapper for the entire module’s workflow. It comprises five key components that work together to achieve the desired outcome. The main steps involved in the workflow are described in the order of execution as follows:

Important

1. Create configuration file. The first step involves creating a configuration file that captures all the specified inputs provided by the user as arguments when running qlimr.py. This process generates a YAML file named config.yaml inside the input folder, reflecting the data supplied by the user. Any flag arguments not provided will be left blank. Within this file, three main YAML keys categorize the input parameters: \(\texttt{input}\), \(\texttt{options}\), and \(\texttt{outputs}\).

2. Validate the input data. Once the configuration file has been created, the next step is to validate the input parameters provided by the user. The wrapper will execute a Python script named Validator.py, which reads the config.yaml file generated in the previous step. This script checks the validity of the input data against a well-established specification outlined in a YAML file called OpenAPI_Specifications_QLIMR.yaml. This specification defines the variable data types for all inputs and outputs. The validator compares the user-provided information against these specifications, ensuring that the correct data types (e.g., double or string) are used. If a data type mismatch occurs, the workflow will stop, requiring the user to provide a correct input value. If any input value is missing or falls outside the valid domain, default values will be used, as detailed in the input section. Upon completion of the validation process, a new file named config_validated.yaml will be created. This file will contain all the input parameters provided by the user, along with the default values filled in for any previously blank spaces in the config.yaml file. This validated file will be used by the C++ source code.

3. Pre-process the given EoS. The next step is to prepare the EoS data file provided by the user for use in the C++ source code. The wrapper will execute another Python script named preprocess.py. This script first checks if a file is provided that adheres to the established conventions and formats (refer to the input section for more information). The naming convention for this file is always eos in either .csv or .h5 format. At the end of this step, a new validated file called eos_validated.csv will be created, containing only two columns: the first for total energy density \(\varepsilon\) and the second for pressure \(p\). If the user has already provided an EoS file with the same name and the correct two-column format, using a comma as the separator, this part of the workflow will be skipped.

4. Execute the C++ source code. The next step is to execute the most critical part of the workflow. The wrapper will run the C++ source code executable named qlimr, which was created during the Dockerfile instructions. This executable computes all the quantities requested by the user, displays the results of the global observables on the screen, and creates two types of output files in the output folder. The first file, observables.csv, contains all the global quantities, while multiple files named local_functions_#.csv are generated, each containing the local functions corresponding to different values of the central energy density. For detailed information about the implementation and structure of the source code, please refer to the source code subsection.

5. Post-process the output. The final step is to post-process the output data. The wrapper will execute a Python script called postprocess.py, which converts observables.csv to HDF5 format if requested by the user through the input flag parameters.

To summarize the ideas presented in this subsection, below is a flowchart that represents the entire process of building the container and the workflow contained in the wrapper script.

Source code

This subsection explains the implementation of the source code, detailing the input parameter options available to the user and describing the outputs, including their column conventions.

Implementation

The primary goal of this module is to compute gravitational observables based on a barotropic equation of state (EoS). The functionality of the source code can be categorized into two cases depending on user needs:

Important

A. Sequence of Neutron Stars Calculation: The user wants to compute global quantities and local functions for an entire sequence specified by a range of central energy densities and a resolution in mass. The specified resolution means that the mass difference between adjacent data values in the sequence should be less than the provided value.

B. Single Star Calculation: The user wants to compute global quantities and local functions for a single neutron star, defined by a specified central energy density.

In both cases, the code allows users to select which observables they wish to compute and whether they want to obtain the local functions. To obtain the observables, it is necessary to solve the ordinary differential equations (ODEs) based on the EoS input data. The general approach is as follows:

Note

1. Read the Equation of State data file.

2. Interpolate the data imposing monotonicity.

3. Compute observables according to the specified case.

4. Export output quantities in the desired format.

To achieve this, the source code is organized into different header files (.hpp) with their corresponding .cpp files, each performing specific tasks. Descriptions of the main tasks associated with each file are provided below, presented in the same order as the execution of the source code. If users want detailed information about every method and function in each class contained in those files, they can refer to the source code itself, which is commented for that purpose.

A_Input : This is the first step in the calculation process. Its main goal is to read the user’s input, as specified by the provided parameters, and to read the EoS file data, converting it into dimensionless values (see the units in one of the appendices).

B_Interpolation : After the Equation of State has been read and converted into dimensionless units, Steffen’s method is employed for interpolation. This method guarantees monotonicity, enabling us to accurately compute \(p(h)\) and \(\varepsilon(h)\), which are essential for solving the TOV equations in pseudo-enthalpy form. A key component of this part of the code is the initialize function, which is used to interpolate all relevant ODE solutions throughout the code.

C_Zeroth_Order : This section of the code solves the TOV equations in pseudo-enthalpy form. It includes the integrator and sets the initial conditions for the problem. The variables \(\texttt{NS_R}\) and \(\texttt{NS_M}\) represent the radius and mass of the neutron star, respectively. These variables are computed after solving the ODE system by evaluating the solutions \(M(h)\) and \(R(h)\) at the surface when \(h=0\). Upon completing this routine, the following local functions are obtained: \(p(R)\) , \(\varepsilon(R)\), \(M(R)\), and \(\nu(R)\).

D_First_Order : This section of the code uses the solutions of the TOV system to solve a second-order ODE, which enters at order \(\mathcal{O}(\epsilon)\). It includes the integrator for this ODE and sets the initial conditions to obtain \(\varpi^{(1)}_{1}(R)\) and \(\varpi'^{(1)}_{1}(R)\) as the solutions. Once these functions are obtained, the code computes the dimensionless moment of inertia, referred to as \(\texttt{NS_Ibar}\).

E_Second_Order : This section of the code handles the equations that enter at order \(\mathcal{O}(\epsilon^{2})\). It includes two integrators for solving \(h^{(2)}_{2}\) and \(k^{(2)}_{2}\) for the \(\ell=2\) mode: the homogeneous and inhomogeneous integrators, along with the initial conditions of the problem. For the \(l=0\) mode, there is another integrator for solving the \(\xi^{(2)}_0\) and \(m^{(2)}_0\) system, as well as an integrator for the function \(y\), which is used to obtain the tidal deformability. After solving these systems, the code calculates the dimensionless tidal Love number \(\bar{\lambda}\), the dimensionless quadrupole moment, \(\bar{Q}\) and the corrections to the radius \(\delta R_{\star}\) and mass \(\delta M_{\star}\). These quantities are stored in the following variables: \(\texttt{NS_Lbar}\), \(\texttt{NS_Qbar}\), \(\texttt{NS_dR}\), and \(\texttt{NS_dM}\), respectively. By solving all these equations, this part of the code computes the folllowing local functions: \(y(R)\), \(h^{(2)}_2(R)\), \(k^{(2)}_2(R)\), \(m^{(2)}_2(R)\), \(\xi^{(2)}_2(R)\), \(m^{(0)}_2(R)\), \(\xi^{(0)}_2(R)\), and \(h^{(0)}_2(R)\).

F_Observables : This section of the code manages the application of previously defined methods based on user requests. Depending on the combination of global quantities specified, a subroutine optimizes the calculation of the ODEs implemented earlier. For example, if the user requests only the tidal Love number, there is no need to compute all the other second-order ODEs; instead, only the TOV system needs to be solved. This optimization applies to all potential combinations of requests. Additionally, when the user selects Case A, this part of the code not only handles the mass resolution but also outputs the local functions and the stable branch if requested. Thus, this section establishes the case type and solves the problem in an optimized manner.

G_Output : This final section is responsible for exporting the outputs in the user-requested format, either .csv or .h5, while also displaying the global quantities on the screen. Additionally, it generates a file named status.yaml, which contains a code indicating whether the entire execution was successful. This code can be read by the calculation engine, providing a means to track any errors originating from the source code.

Attention

Internal Class Dependencies: The dependencies between classes are straightforward; each class in a header file relies on the classes defined in the preceding header files. This sequential dependency is crucial, as solving the equations at a higher order requires the results from the previous orders.

The following flowchart illustrates the overall design of the source code and summarizes its functionality. The left branch represents Case A, while the right branch represents Case B. The resolution algorithm for Case A is presented below the flowchart.

RESOLUTION ALGORITHM

1. Create an initial set. The first step involves selecting a set of central energy densities to compute the neutron star (NS) sequence. The initial distribution in the source code is fixed at \(n=20\) values, arranged on a logarithmic scale. This distribution is determined based on the user’s specified initial and final central energy densities for the sequence.

   The set of central energy densities can be represented mathematically as

   \[\begin{equation} \boldsymbol{\varepsilon}^{(0)}_{c} = \{\varepsilon^{(0)}_{c,1}, \, \varepsilon^{(0)}_{c,2}, \, ..., \, \varepsilon^{(0)}_{c,n} \} \ . \end{equation}\]

   Here, the superscript \((0)\) indicates that this is the initial vector from which the sequence begins, while the subindex \(i\) in \(\varepsilon^{(0)}_{c,i}\) labels the different values in the set. Specifically, \(\varepsilon^{(0)}_{c,1}\) represents the initial value of central energy density specified by the user, and \(\varepsilon^{(0)}_{c,n}\) denotes the final value.

2. Get observables. Every initial condition specified by a central energy density yields a neutron star solution. The second step is to compute the gravitational observables requested by the user for each value in the previously defined set. We will assume the user is interested in all possible global quantities. These can be represented as follows,

   \[\begin{split}\begin{align} \mathbf{A}^{(0)}_{1} &= \{ \varepsilon^{(0)}_{c,1}, \, R_{\star,1}^{(0)}, \, M_{\star,1}^{(0)}, \, \bar{I}^{(0)}_{1}, \, \bar{\lambda}^{(0)}_{1}, \, \bar{Q}^{(0)}_{1}, \delta R_{\star, 1}^{(0)}, \, \delta M_{\star, 1}^{(0)}\} \ , \\[2ex] \mathbf{A}^{(0)}_{2} &= \{ \varepsilon^{(0)}_{c,2}, \, R_{\star,2}^{(0)}, \, M_{\star,2}^{(0)}, \, \bar{I}^{(0)}_{2}, \, \bar{\lambda}^{(0)}_{2}, \, \bar{Q}^{(0)}_{2}, \delta R_{\star, 2}^{(0)}, \, \delta M_{\star, 2}^{(0)}\} \ , \\[1ex] &\vdots \\[1ex] \mathbf{A}^{(0)}_{n} &= \{ \varepsilon^{(0)}_{c,n}, \, R_{\star,n}^{(0)}, \, M_{\star,n}^{(0)}, \, \bar{I}^{(0)}_{n}, \, \bar{\lambda}^{(0)}_{n}, \, \bar{Q}^{(0)}_{n}, \delta R_{\star, n}^{(0)}, \, \delta M_{\star,n}^{(0)}\} \ .\\[2ex] \end{align}\end{split}\]

3. Check resolution. Once we have computed all the observables from the initial set \(\boldsymbol{\varepsilon}^{(0)}_{c}\), we need to verify whether the resolution in mass is sufficient. Specifically, this means checking that the difference in mass between adjacent points on the mass-radius curve is less than the specified resolution provided by the user. If this condition is not met for any pair of points, we must add a new point between those values. This involves selecting a new central energy density that yields a mass value within the interval that does not meet the resolution criteria.

   One possible way to create that new value is by taking the average of the central energy densities that correspond to the two masses being checked. This can be expressed mathematically as:

   \[\begin{split}\begin{align} &\mathsf{If} \ \ \lvert M_{i+1} - M_{i} \rvert > \Delta M^{\textrm{(user)}} \\[2ex] &\mathsf{Create} \ \ \varepsilon^{(1)}_{c,i} = \dfrac{\varepsilon^{(0)}_{c,i+1} + \varepsilon^{(0)}_{c,i}}{2} \\[2ex] &\mathsf{Add \ to} \ \ \boldsymbol{\varepsilon}^{(1)}_{c} . \end{align}\end{split}\]

   Here, \(M_{i+1}\) is the mass obtained given the central energy density \(\varepsilon^{(0)}_{c,i+1}\), and \(M_{i}\) is the mass obtained from \(\varepsilon^{(0)}_{c,i}\). The algorithm must check the resolution in mass for every pair of adjacent points. Whenever it finds that the resolution is not met, it will create a new value of central energy density and add it to the new set \(\boldsymbol{\varepsilon}^{(1)}_{c}\). At the end, we obtain a new set of central energy densities given by

   \[\begin{equation} \boldsymbol{\varepsilon}^{(1)}_{c} = \{\varepsilon^{(1)}_{c,1}, \, \varepsilon^{(1)}_{c,2}, \, ..., \, \varepsilon^{(1)}_{c,m} \} \ . \end{equation}\]

where \(m \leq n-1\).

4. Get observables. Since a new set of central energy densities has been generated, it can be used to compute all observables again. This will yield a new set in which additional points on the mass-radius curve are obtained to improve resolution. The new set can be expressed as follows,

   \[\begin{split}\begin{align} \mathbf{A}^{(1)}_{1} &= \{ \varepsilon^{(1)}_{c,1}, \, R_{\star,1}^{(1)}, \, M_{\star,1}^{(1)}, \, \bar{I}^{(1)}_{1}, \, \bar{\lambda}^{(1)}_{1}, \, \bar{Q}^{(1)}_{1}, \delta R_{\star, 1}^{(1)}, \, \delta M_{\star, 1}^{(1)}\} \ , \\[2ex] \mathbf{A}^{(1)}_{2} &= \{ \varepsilon^{(1)}_{c,2}, \, R_{\star,2}^{(1)}, \, M_{\star,2}^{(1)}, \, \bar{I}^{(1)}_{2}, \, \bar{\lambda}^{(1)}_{2}, \, \bar{Q}^{(1)}_{2}, \delta R_{\star, 2}^{(1)}, \, \delta M_{\star, 2}^{(1)}\} \ , \\[1ex] &\vdots \\[1ex] \mathbf{A}^{(1)}_{m} &= \{ \varepsilon^{(1)}_{c,m}, \, R_{\star,m}^{(1)}, \, M_{\star,m}^{(1)}, \, \bar{I}^{(1)}_{m}, \, \bar{\lambda}^{(1)}_{m}, \, \bar{Q}^{(1)}_{m}, \delta R_{\star, m}^{(1)}, \, \delta M_{\star,m}^{(1)}\} \ .\\[2ex] \end{align}\end{split}\]

5. Stack and sort. Given the two sets of observables \(\mathbf{A}^{(0)}_{i}\) and \(\mathbf{A}^{(1)}_{i}\), the next step is to combine the two sets into one and sort the data in order of increasing energy density. This process will result in a new sorted set that looks like,

   \[\begin{split}\begin{align} \mathbf{A}^{(0)}_{1} &= \{ \varepsilon^{(0)}_{c,1}, \, R_{\star,1}^{(0)}, \, M_{\star,1}^{(0)}, \, \bar{I}^{(0)}_{1}, \, \bar{\lambda}^{(0)}_{1}, \, \bar{Q}^{(0)}_{1}, \delta R_{\star, 1}^{(0)}, \, \delta M_{\star, 1}^{(0)}\} \ , \\[2ex] \mathbf{A}^{(1)}_{1} &= \{ \varepsilon^{(1)}_{c,1}, \, R_{\star,1}^{(1)}, \, M_{\star,1}^{(1)}, \, \bar{I}^{(1)}_{1}, \, \bar{\lambda}^{(1)}_{1}, \, \bar{Q}^{(1)}_{1}, \delta R_{\star, 1}^{(1)}, \, \delta M_{\star, 1}^{(1)}\} \ , \\[2ex] \mathbf{A}^{(0)}_{2} &= \{ \varepsilon^{(0)}_{c,2}, \, R_{\star,2}^{(0)}, \, M_{\star,2}^{(0)}, \, \bar{I}^{(0)}_{2}, \, \bar{\lambda}^{(0)}_{2}, \, \bar{Q}^{(0)}_{2}, \delta R_{\star, 2}^{(0)}, \, \delta M_{\star, 2}^{(0)}\} \ , \\[1ex] &\vdots \\[1ex] \mathbf{A}^{(1)}_{m} &= \{ \varepsilon^{(1)}_{c,m}, \, R_{\star,m}^{(1)}, \, M_{\star,m}^{(1)}, \, \bar{I}^{(1)}_{m}, \, \bar{\lambda}^{(1)}_{m}, \, \bar{Q}^{(1)}_{m}, \delta R_{\star, m}^{(1)}, \, \delta M_{\star,m}^{(0)}\} \ ,\\[2ex] \mathbf{A}^{(0)}_{n} &= \{ \varepsilon^{(0)}_{c,n}, \, R_{\star,n}^{(0)}, \, M_{\star,n}^{(0)}, \, \bar{I}^{(0)}_{n}, \, \bar{\lambda}^{(0)}_{n}, \, \bar{Q}^{(0)}_{n}, \delta R_{\star, n}^{(0)}, \, \delta M_{\star,n}^{(0)}\} \ .\\[2ex] \end{align}\end{split}\]

6. Repeat. From the newly stacked and sorted set, the algorithm can repeat steps 3 to 5 until the desired resolution is achieved. The entire algorithm is illustrated in the following GIF image

   

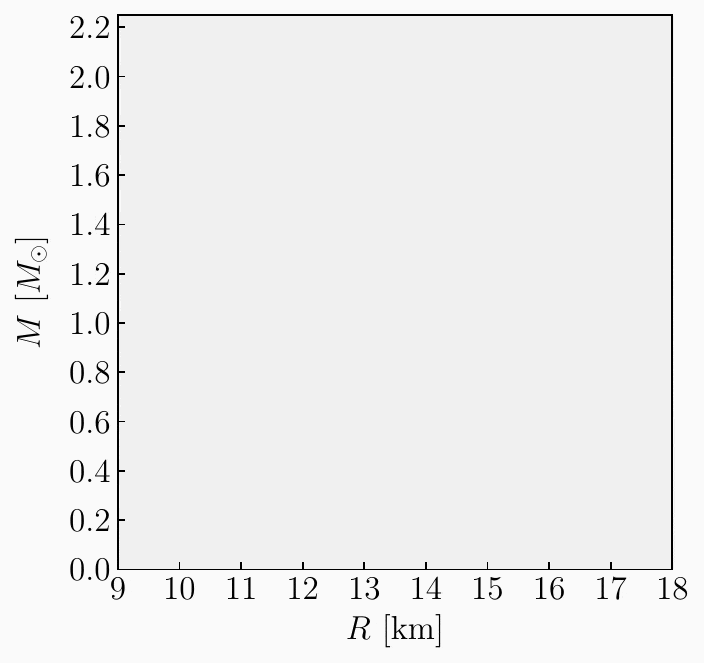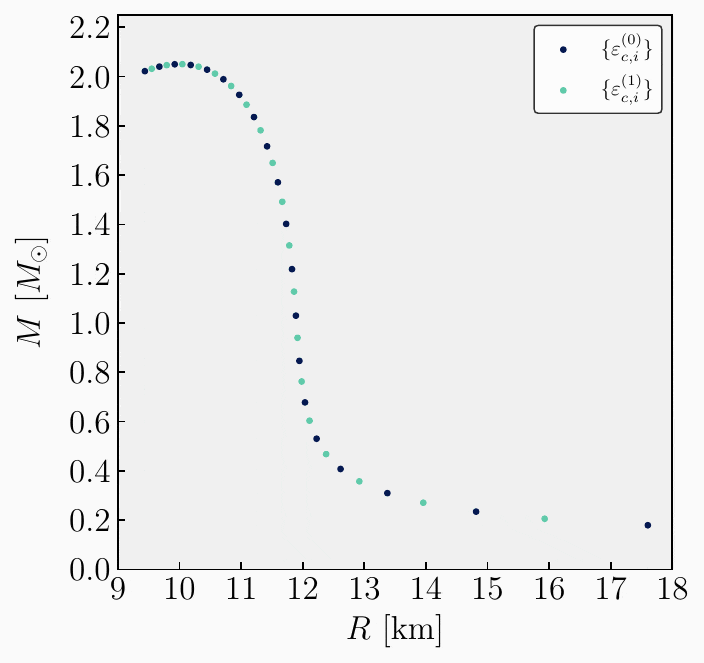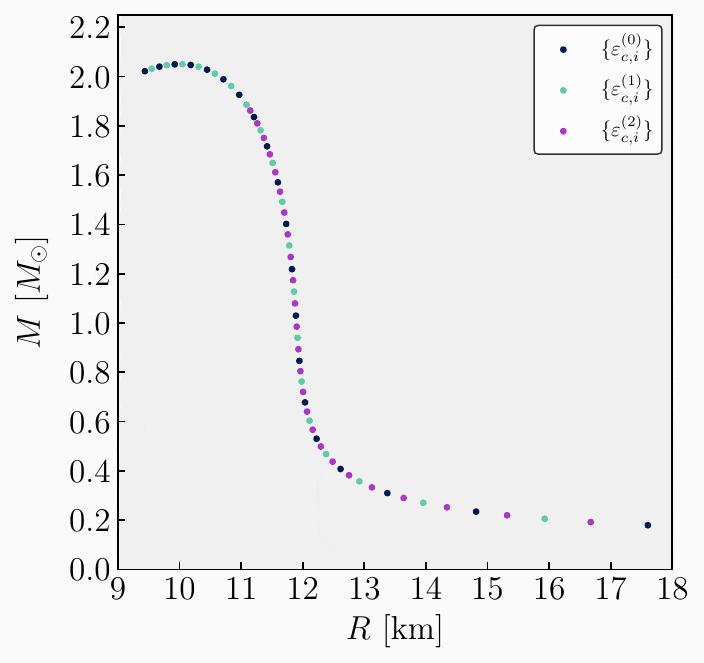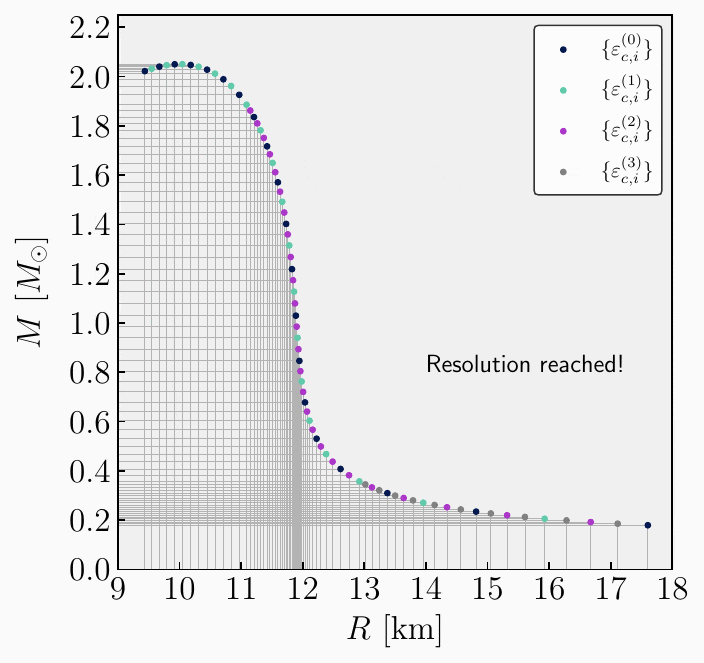
Inputs

This subsection outlines the input conventions for the EoS table that users must provide, as well as the input flag parameters available when using the module.

EOS DATA FILE

Users can offer two types of EoS table conventions. The first is the MUSES EoS table convention, which consists of ten columns detailed as follows, with each column separated by a comma:

Column	Name	Symbol	Unit
1	Temperature	\(T\)	\(\text{MeV}\)
2	Baryon chemical potential	\(\mu_{B}\)	\(\text{MeV}\)
3	Strange chemical potential	\(\mu_{S}\)	\(\text{MeV}\)
4	Charge chemical potential	\(\mu_{Q}\)	\(\text{MeV}\)
5	Baryon number density	\(n_{B}\)	\(\text{fm}^{-3}\)
6	Strangenes number density	\(n_{S}\)	\(\text{fm}^{-3}\)
7	Charge number density	\(n_{Q}\)	\(\text{fm}^{-3}\)
8	Total energy density	\(\varepsilon\)	\(\text{MeV/fm}^{3}\)
9	Pressure	\(p\)	\(\text{MeV/fm}^{3}\)
10	Entropy	\(s\)	\(\text{fm}^{-3}\)

Files should be named eos and can be in either .csv or .h5 format. Alternatively, users may provide a validated EoS data file named eos_validated.csv in the following format, with columns also separated by a comma:

Column	Name	Symbol	Unit
1	Total energy density	\(\varepsilon\)	\(\text{MeV/fm}^{3}\)
2	Pressure	\(p\)	\(\text{MeV/fm}^{3}\)

INPUT PARAMETERS

The table below summarizes all input parameters, including their descriptions and default values. These parameters are provided by the user as arguments when running qlimr.py. For more detailed information, please refer to the explanations provided beneath the table.

Flag Parameter	Description	Default
\(\texttt{--eos_name}\)	Equation of state name	–
\(\texttt{--R_start}\)	Initial radius for integration	0.0004
\(\texttt{--initial_epsilon}\)	Initial value of central energy density	200.0
\(\texttt{--final_epsilon}\)	Final value of central energy density	∞
\(\texttt{--resolution_in_NS_M}\)	Resolution in neutron star mass	0.05
\(\texttt{--single_epsilon}\)	Single value of central energy density	700.0
\(\texttt{--wb11_c}\)	Initial value of dragging function	0.1
\(\texttt{--A22_int}\)	Asymptotic constant at 2nd order	1.0
\(\texttt{--output_format}\)	Output format	csv
\(\texttt{--eps_sequence}\)	Enable epsilon sequence output	true
\(\texttt{--stable_branch}\)	Enable computation on stable branch	true
\(\texttt{--compute_inertia}\)	Compute dimensionless inertia	false
\(\texttt{--compute_love}\)	Compute tidal Love number	false
\(\texttt{--compute_quadrupole}\)	Compute dimensionless quadrupole	false
\(\texttt{--compute_mass_and_radius_correction}\)	Compute mass and radius correction	false
\(\texttt{--local_functions}\)	Enable computation of local functions	false

\(\texttt{--eos_name}\): This option allows the user to specify a name for the Equation of State (EoS) used to compute gravitational observables. This information will be stored in the configuration YAML files, enabling users to recall which EoS was employed in their calculations. This flag is required to run the module when executing qlimr.py.

\(\texttt{--R_start}\): This parameter represents the initial value of the radial coordinate at which the integration of the ODE systems begins. Since all equations diverge exactly at the origin, a very small value—not exactly zero—is chosen for practical numerical integration. The solution from the center up to this selected value can be derived from the asymptotic expansion described in the physics overview section. The units for this parameter are in kilometers (km), and the default value is 0.0004 km.

\(\texttt{--initial_epsilon}\): If the user wishes to compute a neutron star sequence, this flag specifies the initial value of the central energy density to start the sequence, expressed in units of (MeV/fm³). If not provided, this entry defaults to a value of 200 MeV/fm³. It is important to note that if a smaller value is chosen, the resulting neutron star solutions will yield very large radii with correspondingly low masses.

\(\texttt{--final_epsilon}\): This parameter specifies the final value of the neutron star sequence, expressed in units of (MeV/fm³). If not provided, the module will use the maximum energy density value from the EoS data file. Thus, by default, this option ensures the exploration of all possible neutron stars based on the given data. This is important because some equations of state (EoS) may exhibit multiple stable branches, which can only be identified by exploring the entire allowed parameter space of central energy densities from the EoS data file.

\(\texttt{--resolution_in_NS_M}\): This option specifies the resolution in the TOV mass for an entire neutron star sequence. The value of this parameter indicates that there will be no difference in mass between adjacent neutron star solutions on the mass-radius (MR) curve that exceeds the specified value. It is measured in solar masses, and the default value is set to 0.05 \(M_{\odot}\).

\(\texttt{--single_epsilon}\): Each value of central energy density yields a neutron star solution. If the user wishes to compute only one neutron star and its properties, they can provide a single value of central energy density while disabling the neutron star sequence option. The units for this parameter should be given in mega electron-volts per cubic femtometer (MeV/fm³). By default, when eps_sequence is set to false and no value is specified, the parameter takes 700 MeV/fm³.

\(\texttt{--wb11_c}\): This parameter defines the value of the dragging function at the center of the neutron star (\(\varpi_{c}\)). Each chosen value corresponds to a star rotating with a specific angular speed. However, in practice, this value is not critically important, as the outputs are presented in terms of invariant quantities that are normalized with respect to the angular speed \(\Omega\). Generally, this quantity has dimensions of one over time or one over length in geometric units. For this input variable, the units are taken to be dimensionless (neutron star units). For more details, see the appendix on units. The default value is set to 0.1.

\(\texttt{--A22_int}\):This parameter is a constant that appears in the asymptotic analysis around the center of the neutron star for the :math:ell=2 perturbation equations at \(\mathcal{O}(\epsilon^{2})\). It has units of one over length squared; however, the input units are dimensionless, as it is normalized with respect to the characteristic length. In practice, this value is not critically important, as it is primarily used to find the particular solutions of the ODE system for \(h^{(2)}_{2}\) and \(k^{(2)}_{2}\). The default value is set to 1.0.

\(\texttt{--output_format}\): This option allows the user to choose between .csv or .h5 formats for the global quantities, meaning the user will obtain either observables.csv or observables.h5 depending on their preference. These are the formats currently handled by the MUSES collaboration. If not specified, the default value is .csv. For local functions, the format is always .csv at this point.

\(\texttt{--eps_sequence}\): This is an option that accepts only 1 or 0 (or true and false). It indicates whether the user wants to compute an entire neutron star sequence or just a single neutron star solution. If not specified in the arguments, its default value is true, meaning that by default, qlimr.py always runs a neutron star sequence.

\(\texttt{--stable_branch}\): This parameter has two options: 1 or 0 (true or false). It allows the user to obtain the entire neutron star sequence, including unstable regions (when set to false), or only the stable branch along the mass-radius (MR) curve. If no information is provided by the user, only stable stars within the specified domain will be included in the final output file. The default value is true, meaning that the output file will contain only stable branches.

\(\texttt{--compute_inertia}\): This parameter has two options: 1 or 0 (true or false). When set to true, in addition to the radius and mass, it computes the dimensionless moment of inertia, given in geometrical units by

\[\begin{equation} \bar{I} \equiv I/M_{\star}^{3} \, , \end{equation}\]

where \(M_{\star}\) is the TOV mass. By default, this option is set to false.

\(\texttt{--compute_love}\): This parameter has two options: 1 or 0 (true or false). When activated, it computes the dimensionless tidal Love number \(\bar{\lambda}^{(\text{tid})}\) (also known as tidal deformability), given in geometrical units by

\[\begin{equation} \bar{\lambda}^{(\text{tid})} \equiv \dfrac{ \lambda^{(\text{tid})}}{M^{5}_{\star}} = \dfrac{2}{3}k^{(\text{tid})}_{2}C^{-5} \end{equation}\]

where \(k^{(\text{tid})}_{2}\) is known as the tidal apsidal constant and \(C\) is the \(C \equiv M_{\star}/R_{\star}\) compactness. By default, this flag parameter is set to false unless activated by the user.

\(\texttt{--compute_quadrupole}\): This parameter has two options: 1 or 0 (true or false). It is used to compute the dimensionless quadrupole moment deformation of the star due to its rotation. It is defined in geometrical units by

\[\begin{equation} \bar{Q} \equiv \dfrac{Q^{(\text{rot})}}{M^{3}_{\star} \chi^{2}} \end{equation}\]

where is the dimensionless spin parameter given by \(\chi \equiv S/M^{2}_{\star}\). By default, this option is set to false unless specified by the user.

\(\texttt{--compute_mass_and_radius_correction}\): This parameter has two options: 1 or 0 (true or false). It is used to compute the first order correction of the TOV mass and radius, which enters at order \(\mathcal{O}(\epsilon^{2})\) in the Hartle-Thorne approximation for the \(\ell=0\) mode. By default, this option is set to false unless specified by the user. Additionally, the corrections are normalized by the square of the angular speed of the neutron star.

\(\texttt{--local_functions}\): This parameter has two options: 1 (true) or 0 (false). If set to 1, it outputs all local functions from the ODE systems used in the perturbation approach, including TOV solutions and metric functions. It will create one file for each central energy density.

Outputs

Global quantites

Given a set of input parameters, the module can generate two types of outputs: global quantities and local functions. The global quantities are saved in a file named observables.csv (or .h5), depending on the requested format, with a comma (,) as the delimiter. The table below outlines the column conventions used for the global quantities:

Column	Name	Symbol	Unit
1	Central energy density	\(\varepsilon_{c}\)	\(\text{MeV/fm}^{3}\)
2	Neutron star radius	\(R_{\star}\)	\(\text{km}\)
3	Neutron star mass	\(M_{\star}\)	\(M_{\odot}\)
4	Dimenstionless moment of inertia	\(\bar{I}\)	\(\text{[-]}\)
5	Dimensionless tidal Love number	\(\bar{\lambda}\)	\(\text{[-]}\)
6	Dimensionless quadrupole moment	\(\bar{Q}\)	\(\text{[-]}\)
7	Radius correction	\(\delta R_{\star}/\Omega^{2}\)	\(\text{km} \, \text{s}^{2}\)
8	Mass correction	\(\delta M_{\star}/\Omega^{2}\)	\(M_{\odot} \, \text{s}^{2}\)

Note that the moment of inertia does not depend on the choice of \(\varpi_{c}\), which yields different values of the neutron star angular speed. This is because the star’s deformation enters at second order in the Hartle-Thorne approximation, making the moment of inertia insensitive to the choice of \(\varpi_{c}\). However, this is not the case for the quadrupole moment and the corrections to mass and radius. The deformation of the star due to its rotation dependends on its rotational speed. To compute the quadrupole deformation of a star for a specific angular speed, the user can perform the following operation in geometrical units,

\[\begin{equation} Q^{ (\text{rot}) }_{\textsf{user}} = \bar{Q} M^{3}_{\star} \chi^{2}_{\textsf{user}} \end{equation}\]

where \(\chi_{\textsf{user}} \equiv S_{\textsf{user}}/M_{\star}^{2} = (I \Omega_{\textsf{user}})/M_{\star}^{2}\). To obtain the corrections of the mass and the radius of the star for a given angular frequency, then

\[\begin{equation} \delta R_{\star}^{\textsf{user}} = \dfrac{\delta R_{\star}}{\Omega^{2}} \Omega_{\textsf{user}}^{2} \hspace{0.5cm} ; \hspace{0.5cm} \delta M_{\star}^{\textsf{user}} = \dfrac{\delta M_{\star}}{\Omega^{2}} \Omega_{\textsf{user}}^{2} \ . \end{equation}\]

Local functions

The other type of output available to the user is the local functions. These are always provided in .csv format, with the filename structured as local_functions_e_#.csv, where ‘#’’ represents the central energy density value. If an entire sequence is specified, the user will obtain multiple local function files corresponding to each central energy density, depending on the mass resolution. Below is the description and conventions for the columns in each local function file.

Column	Name	Symbol	Unit
1	Radial coordinate	\(R\)	\(\text{km}\)
2	Pressure	\(p(R)\)	\(\text{MeV/fm}^{3}\)
3	Energy density	\(\varepsilon(R)\)	\(\text{MeV/fm}^{3}\)
4	Chemical potential	\(\mu(R)\)	\(\text{MeV}\)
5	Baryon number density	\(n(R)\)	\(\text{1/fm}^{3}\)
6	Metric function \(\mathcal{O}(1)\)	\(M(R)\)	\(M_{\odot}\)
7	Metric function \(\mathcal{O}(1)\)	\(\nu(R)\)	\([-]\)
8	Metric function \(\mathcal{O}(\epsilon)\)	\(\varpi^{(1)}_{1}(R)/\Omega\)	\([-]\)
9	Tidal function \(\mathcal{O}(\epsilon^{2})\)	\(y(R)\)	\([-]\)
10	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(h^{(2)}_{2}(R)/\Omega^{2}\)	\(\text{s}^{2}\)
11	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(k^{(2)}_{2}(R)/\Omega^{2}\)	\(\text{s}^{2}\)
12	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(m^{(2)}_{2}(R)/\Omega^{2}\)	\(M_{\odot} \, \text{s}^{2}\)
13	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(\xi^{(2)}_{2}(R)/\Omega^{2}\)	\(\text{km} \, \text{s}^{2}\)
14	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(m^{(2)}_{0}(R)/\Omega^{2}\)	\(M_{\odot} \, \text{s}^{2}\)
15	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(\xi^{(2)}_{0}(R)/\Omega^{2}\)	\(\text{km} \, \text{s}^{2}\)
16	Metric function \(\mathcal{O}(\epsilon^{2})\)	\(h^{(2)}_{0}(R)/\Omega^{2}\)	\(\text{s}^{2}\)

Similarly, the user can multiply by the corresponding desired angular speed of the star to obtain the local functions for that specific rotational configuration. For example,

\[\begin{equation} \varpi^{(1)}_{1, \textsf{user}} = \dfrac{\varpi^{(1)}_{1}}{\Omega} \Omega_{\textsf{user}} \hspace{0.5cm} ; \hspace{0.5cm} h^{(2)}_{2, \textsf{user}} = \dfrac{h^{(2)}_{2}}{\Omega^{2}} \Omega^{2}_{\textsf{user}} \ . \end{equation}\]